Neural Machine Translation by Jointly Learning to Align and Translate 1 项目介绍 本项目采用Pytorch和Torchtext来构建seq2seq模型,以实现论文 Neural Machine Translation by Jointly Learning to Align and Translate 的模型。
2 Introduction 和之前的项目一样,我们先给出一个通用的seq2seq模型。
在上一个模型中,是通过在每个时间步中直接将上下文向量$z$传递给解码器和向全连接层$f$传递上下文向量、嵌入后的输入词$d(y_t)$和隐藏状态$s_t$来减少信息压缩的。
虽然我们减少了一些信息压缩,但是我们的上下文向量仍然需要包含有关源句子的所有信息。在此项目中将通过使用attention来允许解码器在每个解码步骤中使用隐藏状态查看整个源句子。
attention通过以下步骤来进行:
在解码阶段,会在每个时间步计算一个新的加权源向量,并将其用作解码器RNN以及全连接层的输入来进行预测。
3 准备数据 导入模块
1 2 3 4 5 6 7 8 9 10 11 12 13 14 import torchimport torch.nn as nnimport torch.optim as optimimport torch.nn.functional as Ffrom torchtext.datasets import Multi30kfrom torchtext.data import Field, BucketIteratorimport spacyimport numpy as npimport randomimport mathimport time
设置随机种子
1 2 3 4 5 6 7 SEED = 1234 random.seed(SEED) np.random.seed(SEED) torch.manual_seed(SEED) torch.cuda.manual_seed(SEED) torch.backends.cudnn.deterministic = True
加载spacy的德语和英语模型
1 2 spacy_de = spacy.load("en_core_web_sm" ) spacy_en = spacy.load("de_core_news_sm" )
建立分词函数
1 2 3 4 5 6 7 8 9 10 11 12 def tokenize_de (text ): """ Tokenizes German text from a string into a list of strings """ return [tok.text for tok in spacy_de.tokenizer(text)] def tokenize_en (text ): """ Tokenizes English text from a string into a list of strings """ return [tok.text for tok in spacy_en.tokenizer(text)]
建立Field
1 2 3 4 5 6 7 8 9 10 SRC = Field(tokenize=tokenize_de, init_token='<sos>' , eos_token='<eos>' , lower=True ) TRG = Field(tokenize=tokenize_en, init_token='<sos>' , eos_token='<eos>' , lower=True )
加载数据
1 2 train_data, valid_data, test_data = Multi30k.splits(exts = ('.de' , '.en' ), fields = (SRC, TRG))
建立词汇表
1 2 SRC.build_vocab(train_data,min_freq=2 ) TRG.build_vocab(train_data,min_freq=2 )
定义设备
1 device = torch.device('cuda' if torch.cuda.is_available() else 'cpu' )
建立迭代器
1 2 3 4 5 train_iterator,valid_iterator,test_iterator = BucketIterator.splits( (train_data,valid_data,test_data), batch_size=BATCH_SIZE, device=device )
4 建立模型 4.1 Encoder 首先建立编码器。
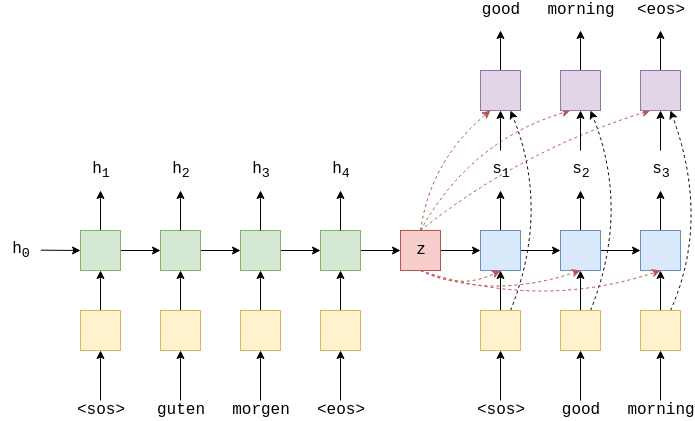
其中$x_0^{\rightarrow}=,x_1^{\rightarrow}=guten,x_0^{\leftarrow}=,x_1^{\leftarrow}=morgen$.
ouputs的大小是[src len,batch size,hid dim*num directions ]。这里的hid dim是前向rnn的隐藏状态,hid dim*num directions可以看作是前向和后向RNN隐藏状态的叠加。比如,$h_1=[h_1^{\rightarrow};h_T^{\leftarrow}],h_2=[h_2^{\rightarrow};h_{T-1}^{\leftarrow}]$,所有的编码器隐藏状态白表示为$\mathbf{H}=\left\{h_{1}, h_{2}, \ldots, h_{T}\right\}$.
hidden的大小是[n_layers*num directions,bathc size,hid dim ],其中[-2,:,:]在最后的时间步(看到最后一个单词)后给出顶层正向RNN隐藏状态。[-1,:,:]在最后的时间步(看到第一个单词之后)之后给出顶层反向RNN隐藏状态。
由于解码器不是双向的,因此只需要一个上下文向量$z$即可用作其初始隐藏状态$s_0$。但是目前我们有两个,前向和后向$z^\rightarrow=h_T^\rightarrow$ and $z^\leftarrow=h_T^\leftarrow$。我们通过将两个上下文向量连接在一起,将他们通过全连接层$g$,然后使用$tanh$激活函数来解决此问题。
这里与论文有些区别,论文中仅通过全连接层提供第一个后向RNN隐藏状态来获取上下文向量和解码器初始隐藏状态。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 class Encoder (nn.Module ): def __init__ (self, input_dim, emb_dim, enc_hid_dim, dec_hid_dim, dropout ): super().__init__() self.embedding = nn.Embedding(input_dim, emb_dim) self.rnn = nn.GRU(emb_dim, enc_hid_dim, bidirectional = True ) self.fc = nn.Linear(enc_hid_dim * 2 , dec_hid_dim) self.dropout = nn.Dropout(dropout) def forward (self, src ): embedded = self.dropout(self.embedding(src)) outputs, hidden = self.rnn(embedded) hidden = torch.tanh(self.fc(torch.cat((hidden[-2 ,:,:], hidden[-1 ,:,:]), dim = 1 ))) return outputs, hidden
4.2 Attention 接下来就是大头了,注意力机制。
可以将其视为计算每个编码器隐藏状态和先前解码器隐藏状态“匹配”的程度。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 class Attention (nn.Module ): def __init__ (self, enc_hid_dim, dec_hid_dim ): super().__init__() self.attn = nn.Linear((enc_hid_dim * 2 ) + dec_hid_dim, dec_hid_dim) self.v = nn.Linear(dec_hid_dim, 1 , bias = False ) def forward (self, hidden, encoder_outputs ): batch_size = encoder_outputs.shape[1 ] src_len = encoder_outputs.shape[0 ] hidden = hidden.unsqueeze(1 ).repeat(1 , src_len, 1 ) encoder_outputs = encoder_outputs.permute(1 , 0 , 2 ) energy = torch.tanh(self.attn(torch.cat((hidden, encoder_outputs), dim = 2 ))) attention = self.v(energy).squeeze(2 ) return F.softmax(attention, dim=1 )
4.3 Decoder 解码器包含注意力层(attention),注意力层输入的是解码层先前隐藏状态$s_{t-1}$和所有编码器隐藏状态$H$,并返回注意力向量$a_t$。weighted 表示,它是使用$a_t$作为权重的编码器隐藏状态$H$的加权和。
接下来,将输入的嵌入$d(y_t)$,加权源向量$w_t$和先前的解码器隐藏状态$s_{t-1}$一起传递到解码器中,,其中$d(y_t)$,$w_t$是串联在一起的。
然后,我们通过全连接层$d(y_t)$,$w_t$和$s_t$,来预测目标句子中的下一个单词,$\hat{y}_{t+1}$。
绿色部分是输出$H$的的双向RNN编码器,红色是上下文向量$z = h_T = \tanh(g(h^\rightarrow_T,h^\leftarrow_T)) = \tanh(g(z^\rightarrow, z^\leftarrow)) = s_0$蓝色是输出$s_t$的RNN解码器。紫色是线性层$f$输出$\hat{y}_{t+1}$ ,橙色是$a_t$对$H$的加权综合计算并输出$w_t$。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 class Decoder (nn.Module ): def __init__ (self, output_dim, emb_dim, enc_hid_dim, dec_hid_dim, dropout, attention ): super().__init__() self.output_dim = output_dim self.attention = attention self.embedding = nn.Embedding(output_dim, emb_dim) self.rnn = nn.GRU((enc_hid_dim * 2 ) + emb_dim, dec_hid_dim) self.fc_out = nn.Linear((enc_hid_dim * 2 ) + dec_hid_dim + emb_dim, output_dim) self.dropout = nn.Dropout(dropout) def forward (self, input, hidden, encoder_outputs ): input = input.unsqueeze(0 ) embedded = self.dropout(self.embedding(input)) a = self.attention(hidden, encoder_outputs) a = a.unsqueeze(1 ) encoder_outputs = encoder_outputs.permute(1 , 0 , 2 ) weighted = torch.bmm(a, encoder_outputs) weighted = weighted.permute(1 , 0 , 2 ) rnn_input = torch.cat((embedded, weighted), dim = 2 ) output, hidden = self.rnn(rnn_input, hidden.unsqueeze(0 )) assert (output == hidden).all() embedded = embedded.squeeze(0 ) output = output.squeeze(0 ) weighted = weighted.squeeze(0 ) prediction = self.fc_out(torch.cat((output, weighted, embedded), dim = 1 )) return prediction, hidden.squeeze(0 )
4.4 Seq2seq 这是第一个不需要编码器RNN和解码器RNN具有相同隐藏尺寸的模型,但是编码器必须是双向的。 可以通过将所有出现的enc_dim 2更改为enc_dim 2(如果encoder_is_bidirectional否则为enc_dim)来消除此要求。
创建输出张量来存放所有的预测$\hat{y}$
源序列$X$被传入编码器来接受$z,H$
解码器的初始隐藏状态被设置为上下文变量,即$s_0=z=h_T$
第一个输入$y_1$被设置为一个batch的
在解码的每个时间步里:
输入初始token$y_t$,上一个隐藏状态$s_{t-1}$,和所有编码器的输出$H$到解码器里
输出预测$\hat{y_{t+1}}$和新的隐藏状态$s_t$
是否需要teacher forcing
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 def __init__ (self, encoder, decoder, device ): super().__init__() self.encoder = encoder self.decoder = decoder self.device = device def forward (self, src, trg, teacher_forcing_ratio = 0.5 ): batch_size = src.shape[1 ] trg_len = trg.shape[0 ] trg_vocab_size = self.decoder.output_dim outputs = torch.zeros(trg_len, batch_size, trg_vocab_size).to(self.device) encoder_outputs, hidden = self.encoder(src) input = trg[0 ,:] for t in range(1 , trg_len): output, hidden = self.decoder(input, hidden, encoder_outputs) outputs[t] = output teacher_force = random.random() < teacher_forcing_ratio top1 = output.argmax(1 ) input = trg[t] if teacher_force else top1 return outputs
5 训练 定义参数
1 2 3 4 5 6 7 8 9 10 11 12 13 OUTPUT_DIM = len(TRG.vocab) ENC_EMB_DIM = 256 DEC_EMB_DIM = 256 ENC_HID_DIM = 512 DEC_HID_DIM = 512 ENC_DROPOUT = 0.5 DEC_DROPOUT = 0.5 attn = Attention(ENC_HID_DIM, DEC_HID_DIM) enc = Encoder(INPUT_DIM, ENC_EMB_DIM, ENC_HID_DIM, DEC_HID_DIM, ENC_DROPOUT) dec = Decoder(OUTPUT_DIM, DEC_EMB_DIM, ENC_HID_DIM, DEC_HID_DIM, DEC_DROPOUT, attn) model = Seq2Seq(enc, dec, device).to(device)
初始化权重
1 2 3 4 5 6 7 8 def init_weights (m ): for name, param in m.named_parameters(): if 'weight' in name: nn.init.normal_(param.data, mean=0 , std=0.01 ) else : nn.init.constant_(param.data, 0 ) model.apply(init_weights)
计算可训练参数
1 2 3 4 def count_parameters (model ): return sum(p.numel() for p in model.parameters() if p.requires_grad) print(f'The model has {count_parameters(model):,} trainable parameters' )
定义激活函数
1 optimizer = optim.Adam(model.parameters())
损失函数
1 2 3 TRG_PAD_IDX = TRG.vocab.stoi[TRG.pad_token] criterion = nn.CrossEntropyLoss(ignore_index = TRG_PAD_IDX)
训练函数
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 model.train() epoch_loss = 0 for i, batch in enumerate(iterator): src = batch.src trg = batch.trg optimizer.zero_grad() output = model(src, trg) output_dim = output.shape[-1 ] output = output[1 :].view(-1 , output_dim) trg = trg[1 :].view(-1 ) loss = criterion(output, trg) loss.backward() torch.nn.utils.clip_grad_norm_(model.parameters(), clip) optimizer.step() epoch_loss += loss.item() return epoch_loss / len(iterator)
评估函数
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 def evaluate (model, iterator, criterion ): model.eval() epoch_loss = 0 with torch.no_grad(): for i, batch in enumerate(iterator): src = batch.src trg = batch.trg output = model(src, trg, 0 ) output_dim = output.shape[-1 ] output = output[1 :].view(-1 , output_dim) trg = trg[1 :].view(-1 ) loss = criterion(output, trg) epoch_loss += loss.item() return epoch_loss / len(iterator)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 def epoch_time (start_time, end_time ): elapsed_time = end_time - start_time elapsed_mins = int(elapsed_time / 60 ) elapsed_secs = int(elapsed_time - (elapsed_mins * 60 )) return elapsed_mins, elapsed_secs N_EPOCHS = 10 CLIP = 1 best_valid_loss = float('inf' ) for epoch in range(N_EPOCHS): start_time = time.time() train_loss = train(model, train_iterator, optimizer, criterion, CLIP) valid_loss = evaluate(model, valid_iterator, criterion) end_time = time.time() epoch_mins, epoch_secs = epoch_time(start_time, end_time) if valid_loss < best_valid_loss: best_valid_loss = valid_loss torch.save(model.state_dict(), 'tut3-model.pt' ) print(f'Epoch: {epoch+1 :02 } | Time: {epoch_mins} m {epoch_secs} s' ) print(f'\tTrain Loss: {train_loss:.3 f} | Train PPL: {math.exp(train_loss):7.3 f} ' ) print(f'\t Val. Loss: {valid_loss:.3 f} | Val. PPL: {math.exp(valid_loss):7.3 f} ' )
6 结果 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 The model has 20,685,396 trainable parameters Using device: cuda TITAN V Memory Usage: Allocated: 0.1 GB Cached: 0.1 GB Epoch: 01 | Time: 0m 41s Train Loss: 5.030 | Train PPL: 152.919 Val. Loss: 4.794 | Val. PPL: 120.778 Epoch: 02 | Time: 0m 41s Train Loss: 4.094 | Train PPL: 59.991 Val. Loss: 4.299 | Val. PPL: 73.631 Epoch: 03 | Time: 0m 40s Train Loss: 3.321 | Train PPL: 27.691 Val. Loss: 3.582 | Val. PPL: 35.934 Epoch: 04 | Time: 0m 41s Train Loss: 2.714 | Train PPL: 15.093 Val. Loss: 3.204 | Val. PPL: 24.619 Epoch: 05 | Time: 0m 41s Train Loss: 2.302 | Train PPL: 9.991 Val. Loss: 3.195 | Val. PPL: 24.400 Epoch: 06 | Time: 0m 41s Train Loss: 1.964 | Train PPL: 7.131 Val. Loss: 3.137 | Val. PPL: 23.039 Epoch: 07 | Time: 0m 41s Train Loss: 1.719 | Train PPL: 5.578 Val. Loss: 3.134 | Val. PPL: 22.957 Epoch: 08 | Time: 0m 41s Train Loss: 1.498 | Train PPL: 4.474 Val. Loss: 3.180 | Val. PPL: 24.047 Epoch: 09 | Time: 0m 41s Train Loss: 1.323 | Train PPL: 3.753 Val. Loss: 3.234 | Val. PPL: 25.378 Epoch: 10 | Time: 0m 41s Train Loss: 1.173 | Train PPL: 3.231 Val. Loss: 3.320 | Val. PPL: 27.656